Turtle graphic 은 우리가 지금 어디있는지 (좌표)는 신경 안쓰고
전진, 방향 회전 단 이 2개 함수로 구현되는 그림을 말합니당
cvs.forward(L, 1);
cvs.turn(89.5);
L 길이 만큼 전진하는데 선을 그린다 (1), 선을 그리지 않는다 (0)
회전 89.5도 입니다
물론 실제로 선 그리는건 vertex2f(x,y) 이기 때문에
현제 바라보는 각도, 현제 절대 좌표 위치 기록을 위한 CD, CP를 둬야하고요;
마치 볼펜 하나 들고 흰 종이에 이어 그린다 라고 생각하시면 편해요(??)
void Canvas::turn(float angle)
{
CD+=angle;
}
void Canvas::forward(float dist, int isVisible)
{
const float RadPerDeg=0.017453373;
float x = CP.getX() + dist * cos(RadPerDeg * CD);
float y = CP.getY() + dist * sin(RadPerDeg * CD);
if(isVisible)
lineTo(x, y);
else moveTo(x, y);
CP.set(x, y);
}
아래 그림은 한선을 그린후 89.5도로 계속 회전하면서 선길이를 0.1씩 늘린 모양입니다.

float L = 1;
for(int i=0; i<500; i++)
{
cvs.forward(L, 1);
cvs.turn(89.5);
L += 0.1;
}
위 그림 같은 것도 그릴 수 있고여
-144도면 오각 별이 그려 집니다.
또 정 n 각형도 각도 계산 해서 하면 간단합니다.
이번엔 Rosette 란걸 그려 봅시당 turtle graphic과는 별 관련 없어요
각점을 연결 시켜야 하기에 위의 turtle graphic과는 달리 각점을 저장해야 합니당
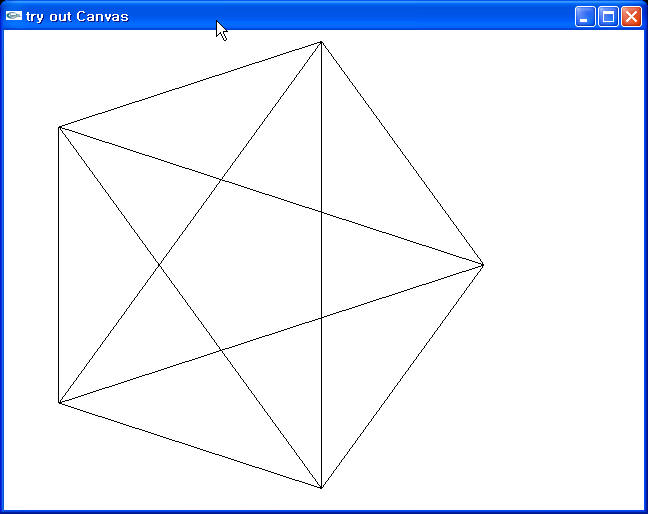
N = 5;
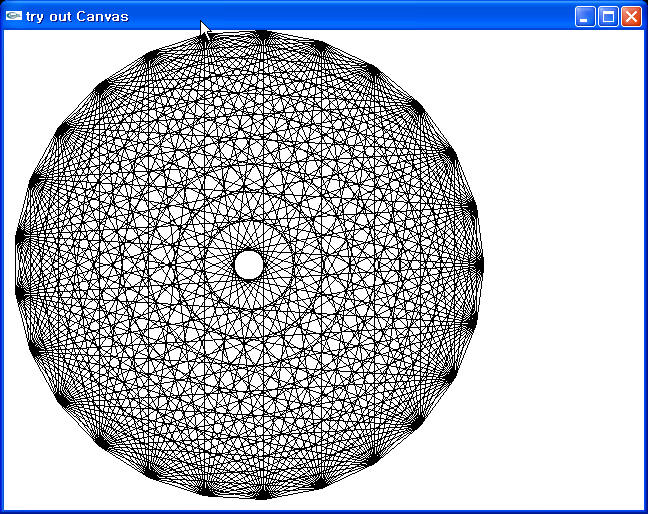
N = 25;
void Canvas::Rosette(int N, float cx, float cy, float radius, float rotAngle)
{
const float PI = 3.14159265;
Point2 pt[100]; // 정 100각형 까지
if(N<3) return; // 2개 짜리 도형은 없음
double angle = rotAngle * PI/ 180; // initial angle
double angleInc = 2* PI / N; // angle increment
// 정 N 각형 좌표 위치를 찾는다.
for(int k = 0; k<=N; k++)
{
angle += angleInc;
// 각 N 각형의 각 점의 위치를 기억한다.
pt[k].set(radius * cos(angle) + cx, radius * sin(angle) + cy);
}
// 각점을 연결한다.
for(int i =0; i < N-1; i++)
for(int j = i+1; j<N; j++)
{
moveTo(pt[i]);
lineTo(pt[j]);
}
}
==================================================================================================
void Canvas::moveTo(const float x, const float y)
{
CP.set(x, y);
}
void Canvas::moveTo(const Point2& pt)
{
moveTo(pt.getX(), pt.getY());
}
void Canvas::lineTo(const float x, const float y)
{
glBegin(GL_LINES);
glVertex2f((GLfloat)CP.getX(), (GLfloat)CP.getY());
glVertex2f((GLfloat)x, (GLfloat)y);
glEnd();
CP.set(x, y);
glFlush();
}
void Canvas::lineTo(const Point2& pt)
{
lineTo(pt.getX(), pt.getY());
}
 invalid-file
invalid-file